RANDOM WALK
La passeggiata aleatoria, è il modello base utilizzato per descrivere i movimenti dei prezzi azionari nei principali modelli di gestione del rischio. È una successione di variabili aleatorie con uguale distribuzione di probabilità e indipendenti l'una dall'altra.
Un esempio elementare di una passeggiata aleatoria semplice è la distribuzione di Bernoulli che assume il valore 1 con probabilità p ( un passo verso destra) e -1 con probabilità 1 - p (un passo verso sinistra) ad ogni passo. Un semplice, discreta, piedi unidimensionale senza pregiudizi la stessa probabilità di andare a destra che a sinistra, vale a dire
 .
.Se sono fatti N realizzazioni, allora abbiamo una distribuzione binomiale:
La distribuzione di probabilità è:
MOTO BROWNIANO
Un processo casuale che descrive il comportamento di alcune variabili casuali lo spostamento nel tempo. Questo processo è spesso usato in modelli finanziari per descrivere l'evoluzione dei prezzi nel tempo. Quando viene applicato ai prezzi, moto browniano presuppone che il passaggio da un periodo all'altro non sono associati con il livello di prezzi oppure a serie storiche delle variazioni dei prezzi. Cioè, ogni variazione di prezzo è indipendente dalle variazioni di prezzo del passato e la volatilità delle variazioni dei prezzi è costante.
In molte indagini simulazione geometrico browniano movimento viene utilizzato per calcolare le probabilità di perdita dopo un certo tempo T, se siete dei titoli che sono i prezzi processi indipendenti o correlate.
TRASFORMAZIONE DI BOX-MULLER
È un metodo per generare coppie di numeri casuali indipendenti e distribuiti gaussianamente con media nulla e varianza uno.
La trasformazione viene comunemente espressa in due forme. La forma principale è quella del lavoro originale: si campionano due numeri dalla distribuzione uniforme sull'intervallo ![(0,1]](http://upload.wikimedia.org/math/6/6/8/668c7b55a37300c330dcd565d9e076da.png) e si ricavano due numeri distribuiti normalmente. La forma polare campiona due numeri su un intervallo differente (
e si ricavano due numeri distribuiti normalmente. La forma polare campiona due numeri su un intervallo differente (![[-1,+1]](http://upload.wikimedia.org/math/3/3/5/335c2d7c2ccfc1766a245197da8da7c8.png) ) e permette di ricavare due numeri distribuiti normalmente senza l'uso delle funzioni seno e coseno.
) e permette di ricavare due numeri distribuiti normalmente senza l'uso delle funzioni seno e coseno.
![(0,1]](http://upload.wikimedia.org/math/6/6/8/668c7b55a37300c330dcd565d9e076da.png) e si ricavano due numeri distribuiti normalmente. La forma polare campiona due numeri su un intervallo differente (
e si ricavano due numeri distribuiti normalmente. La forma polare campiona due numeri su un intervallo differente (![[-1,+1]](http://upload.wikimedia.org/math/3/3/5/335c2d7c2ccfc1766a245197da8da7c8.png) ) e permette di ricavare due numeri distribuiti normalmente senza l'uso delle funzioni seno e coseno.
) e permette di ricavare due numeri distribuiti normalmente senza l'uso delle funzioni seno e coseno.
Siano  e
e 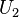 due variabili aleatorie indipendenti ed uniformemente distribuite nell'intervallo
due variabili aleatorie indipendenti ed uniformemente distribuite nell'intervallo ![(0,1]](http://upload.wikimedia.org/math/6/6/8/668c7b55a37300c330dcd565d9e076da.png) . Sia
. Sia
 e
e 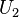 due variabili aleatorie indipendenti ed uniformemente distribuite nell'intervallo
due variabili aleatorie indipendenti ed uniformemente distribuite nell'intervallo ![(0,1]](http://upload.wikimedia.org/math/6/6/8/668c7b55a37300c330dcd565d9e076da.png) . Sia
. Sia
e

Allora Z0 e Z1 sono variabili aleatorie indipendenti con distribuzione normale di deviazione standard unitaria.
La dimostrazione è basata sul fatto che, in un sistema cartesiano bidimensionale nel quale le coordinate X e Y sono descritte da due variabili casuali indipendenti normalmente distribuite, le variabili casuali R2 e  nelle corrispondenti coordinate polari sono a loro volta indipendenti e possono essere espresse come
nelle corrispondenti coordinate polari sono a loro volta indipendenti e possono essere espresse come e
e 
 nelle corrispondenti coordinate polari sono a loro volta indipendenti e possono essere espresse come
nelle corrispondenti coordinate polari sono a loro volta indipendenti e possono essere espresse come e
e